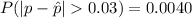Question

A scientist claims that 7% 7 % of viruses are airborne. If the scientist is accurate, what is the probability that the proportion of airborne viruses in a sample of 600 600 viruses would differ from the population proportion by greater than 3% 3 % ? Round your answer to four decimal places.

Answer 1

The probability is
`P(|p-\^(p)| >  0.03)  =   0.0040`

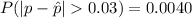
Explanation:

From the question we are told that

The population proportion is
`p =  0.07`

The mean of the sampling distribution is
`\mu_p =  0.07`

The sample size is n = 600

Generally the standard deviation is mathematically represented as

`\sigma_p  =  \sqrt{(p (1 -p))/(n) }`

=>
`\sigma_p  =  \sqrt{(0.07(1 -0.07))/(600) }`

=>
`\sigma_p  =  0.010416`

Generally the probability that the proportion of airborne viruses in a sample of 600 viruses would differ from the population proportion by greater than 3% is mathematically represented as

`P(|p-\^(p)| >  0.03) =  1 - P(|p -\^(p)| \le 0.03)`

=>
`P(|p-\^(p)| >  0.03)  =  1 -  P(-0.03 \le p -\^(p) \le 0.03 )`

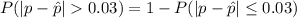
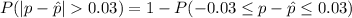
Now add p to both side of the inequality

=>
`P(|p-\^(p)| >  0.03)  =  1 -  P( 0.07-0.03  \le \^(p) \le 0.03+ 0.07 )`

=>
`P(|p-\^(p)| >  0.03)  =  1 -  P(0.04 \le \^(p) \le 0.10 )`

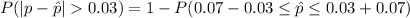
Now converting the probabilities to their respective standardized score

=>
`P(|p-\^(p)| >  0.03)  =  1 -  P((0.04 - 0.07)/(0.010416)  \le Z \le (0.10 -0.07)/(0.010416)  )`

=>
`P(|p-\^(p)| >  0.03)  =  1 -  P(-2.88  \le Z \le 2.88 )`

=>
`P(|p-\^(p)| >  0.03)  =   1 - [P(Z \le 2.88) - P(Z \le -2.88)]`

From the z-table

`P(Z \le 2.88)  =  0.9980`

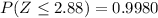
and

`P(Z \le -2.88)  = 0.0020`

So

`P(|p-\^(p)| >  0.03)  =   1 - [0.9980 - 0.0020]`

=>
`P(|p-\^(p)| >  0.03)  =   0.0040`