Question

a car on a circular track accelerates from rest. the radius of the track is 0.30km and the magnitude of the constant angular acceleration is 4.5x10-3 rads/s squared. find the centripetal acceleration of the car when it has completed half of a lap. ​

Answer 1

The centripetal acceleration of the car is 50.4 m/s²

Step-by-step explanation:

Given;

radius of the track, r = 0.3km = 300 m

constant angular acceleration, α = 4.5 x 10⁻³ rad/s²

during half of a lap, θ = π

Determine time of motion

θ = ωt + ¹/₂αt²

π = 0 + ¹/₂αt²

t² = 2π / α

t² = ( 2 x 3.142) / (4.5 x 10⁻³)

t² = 1396.44

t = √1396.44

t = 37.369 s

Determine the angular velocity

`\omega_f = \omega_i + \alpha t\\\\\omega_f = 0 \ + \ 37.369*4.5*10^(-3)\\\\\omega_f = 0.168 \ rad/s`

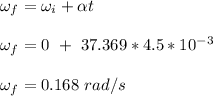
Determine the centripetal acceleration of the car

`\alpha _c = \omega^2 r\\\\\alpha _c = 0.168*300\\\\\alpha _c =50.4 \ m/s^2`

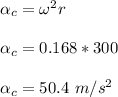
Therefore, the centripetal acceleration of the car is 50.4 m/s²