Question

Hi-Tech, Inc., is a computer training company serving metropolitan Toronto, Canada. The firm contracts a group of part-time instructors to teach a variety of courses concurrently at its downtown location. While demand is so high that any class offered will be filled immediately, Hi-Tech is looking at only two courses at this time: Introduction to Computers (ITC) and Creation of Web Pages (CWP). Each ITC class requires 7.5 hours of preparation/instruction time and contributes a profit of $720, whereas each CWP class calls for only 3 hours and contributes $300. Available time for these two courses is limited to 56 hours a day. There is a restriction on the maximum number of trainees that can be efficiently handled. More specifically, at most 100 students can be accommodated on a daily basis without putting a strain on the facility and support staff. Additionally, each course has a class size limit - 6 for ITC and 12 for CWP. Hi-Tech would like to maximize the daily total profit from both courses so that it could offer certain other courses on a "goodwill" basis. Formulate an AILP for management to decide how many classes should be scheduled for each subject daily

What is the objective function?

Answer 1

The AILP for management to decide how many classes should be scheduled for each subject daily is

The objective function is mathematically represented as

`M  =  P_c  *  a  + P_w  *  b`

=>
`M  = 720  a  + 300  b`

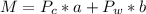
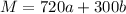
Now the first constraints to this functions is

`t_c  *  x  + t_w * y  \le t_a`

=>
`7.5  x  + 3 y  \le 56`

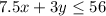
Another constraints to this function is

`k  x  +  u  y  \le  N`

=>
`6  x  +  2  y  \le  100`

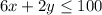
Here x and y are the number of classes

Explanation:

From the question we are told that

The time required for each ITC class is
`t_c  = 7.5 \ hours`

The profit of each ITC class is
`P_c  =  \$ 720`

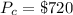
The time require for CWP class is
`t_w  =  3 \  hours`

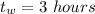
The profit for CWP class is
`P_w  =  \$ 300`

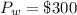
The total time available is
`t_a  =  56 \  hours / day`

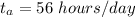
the maximum number of trainee that can be accommodated in a daily basis is
`N  =  100`

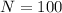
The class size limit for ITC is
`k  =6`

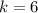
The class size limit for CWP is
`u  =12`

Generally the aim of Hi-Tech is to maximize profit

So the objective function will be a function that maximizes profit

Generally the objective function is mathematically represented as

`M  =  P_c  *  a  + P_w  *  b`

=>
`M  = 720  a  + 300  b`

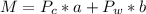
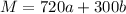
Now the constraints to this functions are

`t_c  *  x  + t_w * y  \le t_a`

=>
`7.5  x  + 3 y  \le 56`

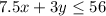
Another constraints to this function is

`k  x  +  u  y  \le  N`

=>
`6  x  +  2  y  \le  100`

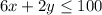
Here x and y are the number of classes