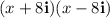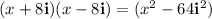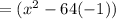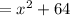Answer:
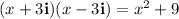
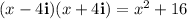
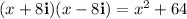
Explanation:
Complex Numbers
The complex numbers are known by having an 'imaginary' part along with the real part. They can be expressed like a + bi, where
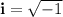
Or, equivalently:

Let's find the result of the following products. On each one of them, there is a sum of a binomial multiplied by the subtraction of a binomial with the very same terms. It leads to a well-known polynomial identity:
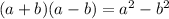
1.
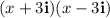
Applying the above-mentioned identity:
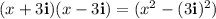
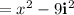
Since


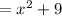
2.
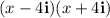
Proceed in the same way as before:
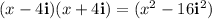
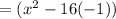
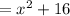
3.