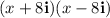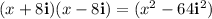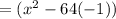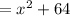Question

Find the product of each expression using properties of complex numbers.

1. (x + 3i)(x − 3i)
2. (x − 4i)(x + 4i)
3. (x + 8i)(x − 8i)

Answer 1

`(x+3\mathbf{i})(x-3\mathbf{i})=x^2+9`

`(x-4\mathbf{i})(x+4\mathbf{i})=x^2+16`

`(x+8\mathbf{i})(x-8\mathbf{i})=x^2+64`

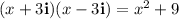
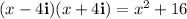
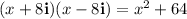
Explanation:

Complex Numbers

The complex numbers are known by having an 'imaginary' part along with the real part. They can be expressed like a + bi, where

`\mathbf{i}=√(-1)`

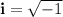
Or, equivalently:

`\mathbf{i}^2=-1`

Let's find the result of the following products. On each one of them, there is a sum of a binomial multiplied by the subtraction of a binomial with the very same terms. It leads to a well-known polynomial identity:

`(a+b)(a-b)=a^2-b^2`

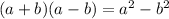
1.
`(x+3\mathbf{i})(x-3\mathbf{i})`

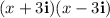
Applying the above-mentioned identity:

`(x+3\mathbf{i})(x-3\mathbf{i})=(x^2-(3\mathbf{i})^2)`

`=x^2-9\mathbf{i}^2`

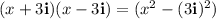
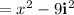
Since
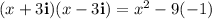
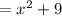
`\mathbf{i}^2=-1`

`(x+3\mathbf{i})(x-3\mathbf{i})=x^2-9(-1)`

`=x^2+9`

2.
`(x-4\mathbf{i})(x+4\mathbf{i})`

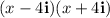
Proceed in the same way as before:

`(x-4\mathbf{i})(x+4\mathbf{i})=(x^2-16\mathbf{i}^2)`

`=(x^2-16(-1))`

`=x^2+16`

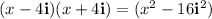
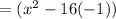
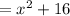
3.
`(x+8\mathbf{i})(x-8\mathbf{i})`

`(x+8\mathbf{i})(x-8\mathbf{i})=(x^2-64\mathbf{i}^2)`

`=(x^2-64(-1))`

`=x^2+64`