Question

NEED HELP ON THIS

If z=-1-i, find z^10 in rectangular form.

The polar form of this problem is 3cis90degrees, what’s the rectangular form?

Answer 1

See below for answers and explanations

Explanation:

Problem 1

Let
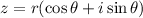`z=r(\cos\theta+i\sin\theta)` be a complex number, where
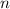`n` is an integer and
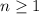`n\geq 1`. By DeMoivre's Theorem, if
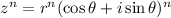`z^n=r^n(\cos\theta+i\sin\theta)^n`, then
`z^n=r^n(\cos n\theta+i\sin n\theta)`.

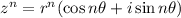Hence, we must first convert from rectangular to polar form:

`z=-1-i\\\\r=√(a^2+b^2)\\\\r=√((-1)^2+(-1)^2)\\\\r=√(1+1)\\\\r=√(2)`

`\displaystyle \theta=\tan^(-1)\biggr((y)/(x)\biggr)\\\\\theta=\tan^(-1)\biggr((-1)/(-1)\biggr)\\ \\\theta=\tan^(-1)(1)\\\\\theta=45^\circ`

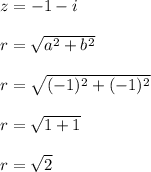
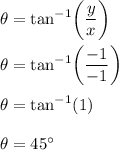
Therefore, the rectangular form for the complex number is
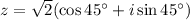`z=√(2)(\cos45^\circ+i\sin45^\circ)`, and now we can apply DeMoivre's Theorem to raise the complex number to the 10th power:

`z=√(2)(\cos45^\circ+i\sin45^\circ)\\\\z^(10)=√(2)^(10)(\cos45^\circ+i\sin45^\circ)^(10)\\\\z^(10)=2^5(\cos10\cdot45^\circ+i\sin10\cdot45^\circ)\\\\z^(10)=32(\cos450^\circ+i\sin450^\circ)\\\\z^(10)=32(0+i)\\\\z^(10)=32i`

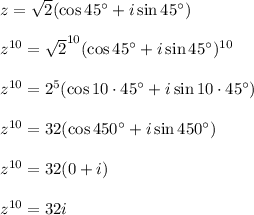
Therefore,
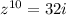`z^(10)=32i` in rectangular form.

Problem 2

`3\:\text{cis}\:90^\circ=3(\cos90^\circ+i\sin90^\circ)=3(0+i)=3i`

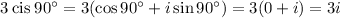
Therefore,
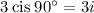`3\:\text{cis}\:90^\circ=3i` in rectangular form.