Answer:
See below for answers and explanations
Explanation:
Problem 1
Let
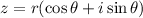 be a complex number, where
be a complex number, where
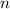 is an integer and
is an integer and
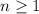 . By DeMoivre's Theorem, if
. By DeMoivre's Theorem, if
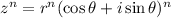 , then
, then
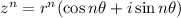 .
.
Hence, we must first convert from rectangular to polar form:
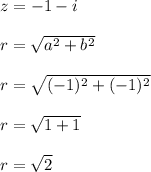
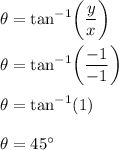
Therefore, the rectangular form for the complex number is
 , and now we can apply DeMoivre's Theorem to raise the complex number to the 10th power:
, and now we can apply DeMoivre's Theorem to raise the complex number to the 10th power:
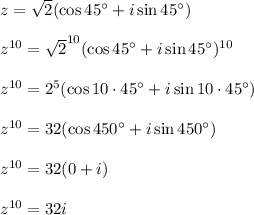
Therefore,
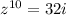 in rectangular form.
in rectangular form.
Problem 2
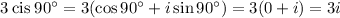
Therefore,
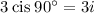 in rectangular form.
in rectangular form.