Answer:
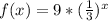
Explanation:
Hello!
Let's break down the formula

Looking at the graph, we can see that
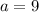 , as it is when x is 0, and is the starting point.
, as it is when x is 0, and is the starting point.
To solve for the multiplier (
 ):
):
- divide the next term by the prevoius term
Multiplier:
- When x = 0, the value is 9
- When x = 1, the value is 3
- 3/9 = 1/3
- The multipler is 1/3
So, plug in the values:
The equation in
 form is
form is
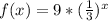 .
.