Question

Check all of the polynomial functions that have 2 as a root.

h(m) = 8 – m3
f(g) = g3 – 2g2 + g
f(a) = a3 – 4a2 + a + 6
f(x) = x3 – x2 – 4

Answer 1

answers are A, C, and D

Explanation:

THIS IS CORRECT

Answer 2

Explained below

Explanation:

Polynomial Roots

If x=a is a root of f(x), then f(a)=0

We will test the following functions to check if a=2 is a root.

• 
  `h(m)=8-m^3`

`h(2)=8-2^3=8-8=0`

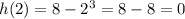
Thus m=2 is a root of h

• 
  `f(g)=g^3-2g^2+g`

`f(2)=2^3-2\cdot 2^2+2`

`f(2)=8-2\cdot 4+2=8-8+2=2`

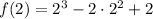
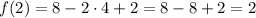
Thus g=2 is not a root of f

• 
  `f(a) = a^3 - 4a^2 + a + 6`

`f(2) = 2^3 - 4\cdot 2^2 + 2 + 6`

`f(2) = 8-16+8=0`

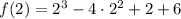
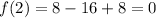
Thus a=2 is a root of f

• 
  `f(x) = x^3 - x^2 - 4`

`f(2)=2^3 - 2^2 - 4`

`f(2)=8 - 4 - 4=0`

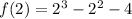
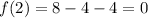
Thus x=2 is a root of f