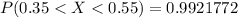Question

Suppose you take a simple random sample of size n=175 from the population of Reese's Pieces, still assuming that 45% of this population is orange (LaTeX: \piπ=.45).

What is the probability that a sample proportion of orange candies will be between .35 and .55?

Answer 1

The probability is
`P(0.35 <X < 0.55) = 0.9921772`

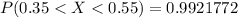
Explanation:

From the question we are told that

The sample size is n = 175

The population proportion is p = 0.45

Generally the mean of the sampling distribution is
`\mu_(x) = 0.45`

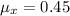
Generally the standard deviation is mathematically represented as

`\sigma_(x) = \sqrt{(p (1-p))/(n) }`

=>
`\sigma_(x) = \sqrt{(0.45 (1-0.45))/(175) }`

=>
`\sigma_(x) = 0.0376`

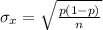
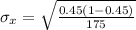
Generally the probability of that the sample proportion of orange candies will be between 0.35 and 0.55 is

`P(0.35 < X < 0.55) = P( (0.35 - 0.45)/(0.0376) < (X -\mu_(x))/(\sigma_(x)) < (0.55 - 0.45)/(0.0376) )`

=>
`P(0.35 <X < 0.55) = P( -2.696 < (X -\mu_(x))/(\sigma_(x)) < 2.6595 )`

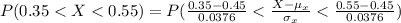
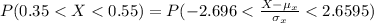
Generally
`(X - \mu_(x))/(\sigma_(x)) = Z (The \ standardized \ value \ of X)`

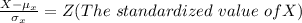
So

`P(0.35 <X < 0.55) = P( -2.6596 < Z< 2.6595 )`

=>
`P(0.35 <X < 0.55) =P( Z< 2.6595 ) - P( Z < -2.6596 )`

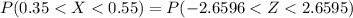
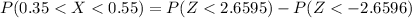
From the z-table

`P( Z< 2.6595 ) = 0.99609`

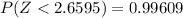
and

`P( Z< - 2.6595 ) = 0.0039128`

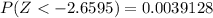
So

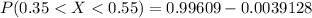
`P(0.35 <X < 0.55) =0.99609 - 0.0039128`

=>
`P(0.35 <X < 0.55) = 0.9921772`