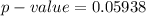Answer:
The test statistics is
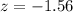
The p-value is
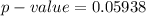
Explanation:
From the question we are told
The West side sample size is

The number of residents on the West side with income below poverty level is
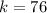
The East side sample size
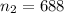
The number of residents on the East side with income below poverty level is
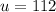
The null hypothesis is
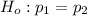
The alternative hypothesis is

Generally the sample proportion of West side is
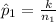
=>

=>
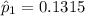
Generally the sample proportion of West side is
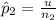
=>
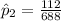
=>

Generally the pooled sample proportion is mathematically represented as
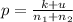
=>
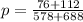
=>
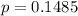
Generally the test statistics is mathematically represented as
![z = \frac{\^ {p}_1 - \^(p)_2}{\sqrt{p(1- p) [(1)/(n_1 ) + (1)/(n_2) ]} }](https://img.qammunity.org/2021/formulas/mathematics/college/uhtlftbsw6mt9dgvxa078gaha0negnjj2l.png)
=>
![z = \frac{ 0.1315 - 0.1628 }{\sqrt{0.1485(1-0.1485) [(1)/(578) + (1)/(688) ]} }](https://img.qammunity.org/2021/formulas/mathematics/college/hxhfeiugg6re5rgxfslzfeqyylse8g5ghb.png)
=>
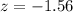
Generally the p-value is mathematically represented as
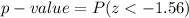
From z-table
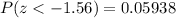
So