The resulting matrix from the elementary row operation -2R2 + 3R1 applied to matrix A =
![\[ \begin{bmatrix} -3 & 5 & 2 \\ 8 & -1 & 3 \end{bmatrix} \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/un7eha2pv40gnxylhl7a5y3c6i59n64jw1.png) is
is
![\[ \begin{bmatrix} -22 & 17 & 0 \\ 8 & -1 & 3 \end{bmatrix} \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/w90tjhzkz285quuf7ol22msprcia7e8hfi.png) .
.
To apply the elementary row operation
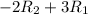 to the matrix A, you perform the following operation on each element:
to the matrix A, you perform the following operation on each element:
![\[ \text{Resulting element} = -2 * \text{Element in row 2} + 3 * \text{Element in row 1} \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/e9dcdo6lkkbu27ftn4mdvia37uz5o9kmys.png)
So, for the given matrix A:
![\[ \text{Resulting matrix} = \begin{bmatrix} -2 * (8) + 3 * (-3) & -2 * (-1) + 3 * 5 & -2 * 3 + 3 * 2 \\ 8 & -1 & 3 \end{bmatrix} \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/btumqm3ylvvtbuq7607isea6pfwu12bmup.png)
Simplifying each element:
![\[ \text{Resulting matrix} = \begin{bmatrix} -22 & 17 & 0 \\ 8 & -1 & 3 \end{bmatrix} \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/kjcep64pak85vulmfq9k2t07t56lfjlbtc.png)
Therefore, the matrix resulting from the elementary row operation is:
![\[ \begin{bmatrix} -22 & 17 & 0 \\ 8 & -1 & 3 \end{bmatrix} \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/w90tjhzkz285quuf7ol22msprcia7e8hfi.png)