Question

Consider matrix A.

What matrix results from the elementary row operations represented by -2R2 + 3Rı?
Enter your answer by filling in the boxes.

Answer 1

I misread the question. Had the elementary row operations been represented by -3R2 + 4R1, then the answer would have been,

-36 23 -1

8 -1 3

hopefully this will still help some of you

Answer 2

The resulting matrix from the elementary row operation -2R2 + 3R1 applied to matrix A =
`\[ \begin{bmatrix} -3 & 5 & 2 \\ 8 & -1 & 3 \end{bmatrix} \]` is
`\[ \begin{bmatrix} -22 & 17 & 0 \\ 8 & -1 & 3 \end{bmatrix} \]`.

To apply the elementary row operation
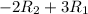`\(-2R_2 + 3R_1\)` to the matrix A, you perform the following operation on each element:

`\[ \text{Resulting element} = -2 * \text{Element in row 2} + 3 * \text{Element in row 1} \]`

So, for the given matrix A:

`\[ \text{Resulting matrix} = \begin{bmatrix} -2 * (8) + 3 * (-3) & -2 * (-1) + 3 * 5 & -2 * 3 + 3 * 2 \\ 8 & -1 & 3 \end{bmatrix} \]`

Simplifying each element:

`\[ \text{Resulting matrix} = \begin{bmatrix} -22 & 17 & 0 \\ 8 & -1 & 3 \end{bmatrix} \]`

Therefore, the matrix resulting from the elementary row operation is:

`\[ \begin{bmatrix} -22 & 17 & 0 \\ 8 & -1 & 3 \end{bmatrix} \]`