Question

Compute the estimated regression's prediction for the average score of students given 98, 129, or 159 minutes to complete the exam.

Given 98 minutes, the estimated regression's prediction for the average score of students is 91.94 .
Given 129 minutes, the estimated regression's prediction for the average score of students is 108.37
Given 159 minutes, the estimated regression's prediction for the average score of students is 124.27 (Round your responses to two decimal places.)
Compute the estimated gain in score for a student who is given an additional 32 minutes on the exam.
The estimated gain in score for a student who is given an additional 32 minutes on the exam is (Round your response to two decimal places.)

Answer 1

The estimated gain in score for a student who is given an additional 32 minutes on the exam is 16.96

Explanation:

The estimated regression prediction is given by:

`\hat{y}=40+0.53x`

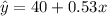
Where x denotes the time

y denotes the average score

A)

Substitute x = 98

`\hat{y}=40+0.53(98) = 91.94`

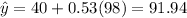
B)

Substitute x = 129

`\hat{y}=40+0.53(129) = 108.37`

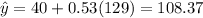
C)

Substitute x = 159

`\hat{y}=40+0.53(159) = 124.27`

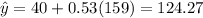
D)the estimated gain in score for a student who is given an additional 32 minutes on the exam.

`\hat{y}=40+0.53(x+32)=40+0.53x+9.57=y+16.96`

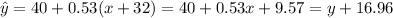
So, the estimated gain in score for a student who is given an additional 32 minutes on the exam is 16.96