Question

Large wind turbines with blade span diameters of over 100 m are available for electric power generation. Consider a wind turbine with a blade span diameter of 100 m installed at a site subjected to steady winds at 8 m/s. Taking the overall efficiency of the wind turbine to be 32 percent and the air density to be 1.25 kg/m3 , determine the electric power generated by this wind turbine. Also, assuming steady winds of 8 m/s during a 24-hour period, determine the amount of electric energy and the revenue generated per day for a unit price of $0.09/kWh for electricity

Answer 1

The wind turbine generates
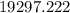`19297.222` kilowatt-hours of electricity daily.

The wind turbine makes a daily revenue of 1736.75 US dollars.

Step-by-step explanation:

First, we have to determine the stored energy of wind (
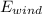`E_(wind)`), measured in Joules, by means of definition of Kinetic Energy:

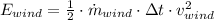`E_(wind) = (1)/(2)\cdot \dot m_(wind)\cdot \Delta t \cdot v_(wind)^(2)` (Eq. 1)

Where:

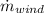`\dot m_(wind)` - Mass flow of wind, measured in kilograms per second.

`\Delta t` - Time in which wind acts in a day, measured in seconds.

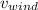`v_(wind)` - Steady wind speed, measured in meters per second.

By assuming constant mass flow and volume flows and using definitions of mass and volume flows, we expand the expression above:

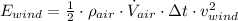`E_(wind) = (1)/(2)\cdot \rho_(air)\cdot \dot V_(air) \cdot \Delta t \cdot v_(wind)^(2)` (Eq. 1b)

Where:

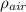`\rho_(air)` - Density of air, measured in kilograms per cubic meter.

`\dot V_(air)` - Volume flow of air through wind turbine, measured in cubic meters per second.

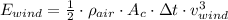`E_(wind) = (1)/(2)\cdot \rho_(air)\cdot A_(c)\cdot \Delta t\cdot v_(wind)^(3)` (Eq. 2)

Where
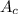`A_(c)` is the area of the wind flow crossing the turbine, measured in square meters. This area is determined by the following equation:

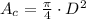`A_(c) = (\pi)/(4)\cdot D^(2)` (Eq. 3)

Where
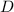`D` is the diameter of the wind turbine blade, measured in meters.

If we know that
`\rho_(air) = 1.25\,(kg)/(m^(3))`,
`D = 100\,m`,
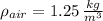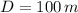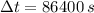`\Delta t = 86400\,s` and
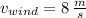`v_(wind) = 8\,(m)/(s)`, the stored energy of the wind in a day is:

`A_(c) = (\pi)/(4)\cdot (100\,m)^(2)`

`A_(c) \approx 7853.982\,m^(2)`

`E_(wind) = (1)/(2)\cdot \left(1.25\,(kg)/(m^(3)) \right) \cdot (7853.982\,m^(2))\cdot (86400\,s)\cdot \left(8\,(m)/(s) \right)^(3)`

`E_(wind) = 2.171* 10^(11)\,J`

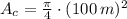
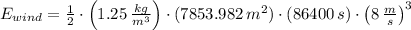
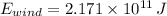
Now, we proceed to determine the quantity of energy from wind being used by the wind turbine in a day (
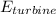`E_(turbine)`), measured in joules, with the help of the definition of efficiency:

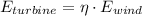`E_(turbine) = \eta\cdot E_(wind)` (Eq. 4)

Where
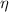`\eta` is the overall efficiency of the wind turbine, dimensionless.

If we get that
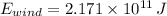`E_(wind) = 2.171* 10^(11)\,J` and
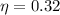`\eta = 0.32`, then the energy is:

`E_(turbine) = 0.32\cdot (2.171* 10^(11)\,J)`

`E_(turbine) = 6.947* 10^(10)\,J`

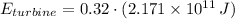
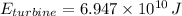
The wind turbine generates
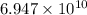`6.947* 10^(10)` joules of electricity daily.

A kilowatt-hours equals 3.6 million joules. We calculate the equivalent amount of energy generated by wind turbine in kilowatt-hours:

`E_(turbine) = 6.947* 10^(10)\,J*(1\,kWh)/(3.6* 10^(6)\,J)`

`E_(turbine) = 19297.222\,kWh`

The wind turbine generates
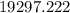`19297.222` kilowatt-hours of electricity daily.

Lastly, the revenue generated per day can be found by employing the following:

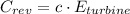`C_(rev) = c\cdot E_(turbine)` (Eq. 5)

Where:

`c` - Unit price, measured in US dollars per kilowatt-hour.

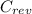`C_(rev)` - Revenue generated by the wind turbine in a day, measured in US dollars.

If we know that
`c = 0.09\,(USD)/(kWh)` and
`E_(turbine) = 19297.222\,kWh`, then the revenue is:

`C_(rev) = \left(0.09\,(USD)/(kWh) \right)\cdot (19297.222\,kWh)`

`C_(rev) = 1736.75\,USD`

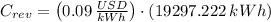
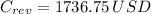
The wind turbine makes a daily revenue of 1736.75 US dollars.