Question

In triangle QRS the measure of right angle S is SQ=90 degrees Sq=47 feet and Rs=70 feet. Find the measure of angle R to the nearest tenth of a degree

Answer 1

x=33.9°

Explanation:

Trigonometric Ratios

In a right triangle, i.e. the triangles that have an internal angle of 90°, the so-called trigonometric ratios are valid.

There are six trigonometric ratios that can be used in right triangles, depending on the data available for each problem.

The current question gives us two sides in a right triangle and requires us to calculate the angle x.

The angle x 'looks' at the sides of the triangle in this way: RS=70 is the adjacent leg, SQ=47 is the opposite leg, and RQ is the hypotenuse.

We should use the trigonometric ratio that relates both the adjacent and the opposite led. There are two possibilities: The tangent and the cotangent. We'll use the tangent for no particular reason.

The tangent of an angle is defined as:

`\displaystyle \tan\x=\frac{\text{opposite leg}}{\text{adjacent leg}}\\`

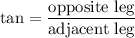
Use the given values:

`\displaystyle \tan x=(47)/(70)=0.6714`

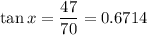
Using a calculator (in degree mode), we calculate the angle:

`x=\tan^(-1)(0.6714)=33.9^\circ`

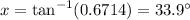
x=33.9°