Options:
Rotation of 180° about point B
Rotation of 90° about point b
Reflection over the x-axis
Translation down 2 units
Answer:
Rotation of 180° about point B
Explanation:
Considering coordinates of point B
Assume the coordinates of the line at point B is (x,y)
i.e.
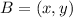
First, we need to determine the slope at point B
Taking coordinates about the origin.
The slope of B is:

Where
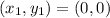 --- origin
--- origin
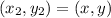
 becomes
becomes
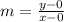
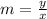
Taking the options one after the other:
Option A.
When rotated by 180°, the resulting coordinates of B would be
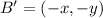
Taking the slope of B'
The slope of B is:

Where
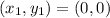 --- origin
--- origin

 becomes
becomes
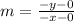

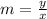
Notice that the slope of B and B' is the same;
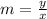
Hence:
Rotation of 180° about point B answers the question
There's no need to check for other options