Answer:
The length of the diagonal of the rectangle is C. 21.25
Explanation:
To find the diagonal of this rectangle, we must use the Pythagorean Theorem.
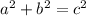 , where a and b are legs and c is the hypotenuse.
, where a and b are legs and c is the hypotenuse.
As we can see the rectangle is divided into two parts, we can make out a right triangle assuming the angle where the two legs meet is 90 degrees.
Given:
a = 12.75
b = 17
Unkown:
c = ?
To find c (aka the Hypotenuse) we can plug in the Pythagorean theorem.
a^2 + b^2 = c^2
12.75^2 + 17^2 = c^2
451.5625 = c^2
c = ± 21.25
In the context of this question, we will use the positive result as lengths cannot be negative.
Answer: C. 21.25