Answers:
Option 1)
6a + 8s = 102
14a + 4s = 150
each adult ticket costs 9 dollars
===================================================
Step-by-step explanation:
6 adult tickets and 8 student tickets bring in $102, so that means 6a+8s = 102
14 adult tickets and 4 students tickets bring in $150, so 14a+4s = 150
The system of equations is
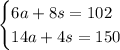
If we multiply both sides of the second equation by -2, we get this updated system
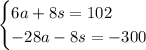
Add the equations straight down
6a+(-28a) = -22a
8s+(-8s) = 0s = 0 ... the 's' terms go away
102+(-300) = -198
So we end up with the equation -22a = -198 and that solves to a = 9 after dividing both sides by -22.
Each adult ticket costs $9
If you want the value of s, then
6a+8s = 102
6(9)+8s = 102
54 + 8s = 102
8s = 102-54
8s = 48
s = 48/8
s = 6
Meaning each student ticket costs $6
Or you could use the other equation
14a+4s = 150
14(9)+4s = 150
126+4s = 150
4s = 150-126
4s = 24
s = 24/4
s = 6
We get the same value of s