Question

4. Suppose that you are offered the following "deal." You roll a die. If you roll a six, you win $10. If you roll a four or five, you win $5. If you roll a one, two, or three, you pay $6. a. What are you ultimately interested in here (the value of the roll or the money you win)? b. In words, define the Random Variable X. c. List the values that X may take on. d. Construct a PDF. e. Over the long run of playing this game, what are your expected average winnings per game? f. Based on numerical values, should you take the deal? Explain your decision in complete sentences.

Answer 1

Explained below.

Explanation:

The rules of the deal are as follows:

• If you roll a six, you win $10.
• If you roll a four or five, you win $5.
• If you roll a one, two, or three, you pay $6.

(a)

The correct option is: "the money you win".

(b)

The random variable X denotes the amount won or lost.

(c)

The value of X are as follows:

X = {-$6, $5 and $10}

(d)

The probability function of X is as follows:

P (X = 10) = 1/6

P (X = 5) = 1/3

P (X = -6) = 1/2

(e)

Compute the expected value as follows:

`E(X)=\sum x* P(X=x)\\`

`=(10*(1)/(6))+(5*(1)/(3))+(-6*(1)/(2))\\\\=0.333333\\\\\approx $0.33`

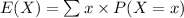
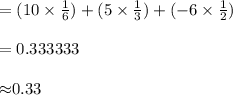
Thus, the average winnings per game is $0.33.

(f)

Since the expected value of the game is a positive amount, the deal will not lead to me paying up.

Thus, you take the deal.