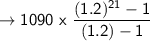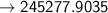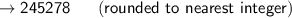Question

On the first day it was posted online, a music video got 1090 views. The number of views that the video got each day increased by 20% per day. How many total views did the video get over the course of the first 21 days, to the nearest whole number?

Answer 1

Answer: 245278 views

Series built : 1090, 1308, 1569.6, 1883.52, 2260.224, 2712.2688,...

As every term increases by 1.2, This is a geometric progression sequence.

`\sf Geometric \ Sequence: a_1 \ x \ (r^n - 1)/(r -1)`

Identify Variable's:

a1 = 1090

r = second term ÷ first term = 1308 ÷ 1090 = 1.2

n = 21

Step-by-step explanation:

`\rightarrow \sf 1090 \ x \ ((1.2)^(21) - 1)/((1.2) -1)`

`\rightarrow \sf 245277.9035`

`\rightarrow \sf 245278 \ \ \ \ \ (rounded \ to \ nearest \ integer)`

Answer 2

• 245278

Step-by-step explanation:

The number of views make a GP since increase 20% or 1.2 times per day

• 1090, 1090*1.2, 1090*1.2², ...

The first term is t = 1090 and common ratio is r = 1.2

Find the sum of the first 21 terms

• Sₙ = t(rⁿ - 1)/(r - 1) = 1090*(1.2²¹ - 1)/(1.2 - 1) = 245278 (rounded)