Answer:
a
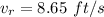
b

Step-by-step explanation:
From the question we are told that
The mass of the ball is
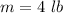
The radius is
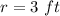
The speed is
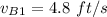
The speed of the attached cord is
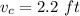
The position that is been considered is
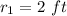 h
h
Generally according to the law of angular momentum conservation
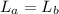
Here
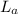 is the initial momentum of the ball which is mathematically represented as
is the initial momentum of the ball which is mathematically represented as
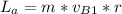
while
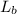 is the momentum of the ball at r = 2 ft which is mathematically represented as
is the momentum of the ball at r = 2 ft which is mathematically represented as

So
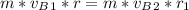
=>

=>
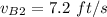
Generally the resultant velocity of the ball is
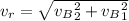
=>
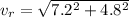
=>
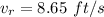
Generally according to equation for principle of work and energy we have that
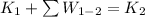
Here
 is the initial kinetic energy of the ball which is mathematically represented as
is the initial kinetic energy of the ball which is mathematically represented as
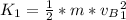
While
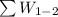 is the sum of the total workdone by the ball
is the sum of the total workdone by the ball
and
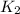 is the final kinetic energy of the ball which is mathematically represented as
is the final kinetic energy of the ball which is mathematically represented as
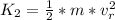
So
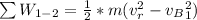
Here m is the mass which is mathematically represented as
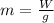 here W is the weight in lb and g is the acceleration due to gravity which is
here W is the weight in lb and g is the acceleration due to gravity which is
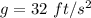
So
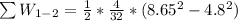
=>
