Question

Assume that we have two events, and , that are mutually exclusive. Assume further that we know and . If an amount is zero, enter "". a. What is ? b. What is ? c. A student in statistics argues that the concepts of mutually exclusive events and independent events are really the same, and that if events are mutually exclusive they must be independent. Do you agree with this statement? Use the probability information in this problem to justify your answer. - Select your answer - , because - Select your answer - . d. What general conclusion would you make about mutually exclusive and independent events given the results of this problem? - Select your answer -

Answer 1

Explained below.

Explanation:

The complete question is:

Assume that we have two events, A and B, that are mutually exclusive. Assume further that we know P(A) = 0.30 and P(B) =0.40.

What is P(A and B)?

What is P(A | B)?

Is P(A | B) equal to P(A)?

Are events A and B dependent or independent?

A student in statistics argues that the concepts of mutually exclusive events and independent events are really the same, and that if events are mutually exclusive they must be independent. Is this statement accurate?

What general conclusion would you make about mutually exclusive and independent events given the results of this problem?

Solution:

The probability of the two events A and B are:

P(A) = 0.30 and P(B) =0.40

(a)

Compute the value of P (A ∩ B) as follows:

`P(A\cap B)=0`

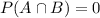
This is because mutually exclusive events are those events that cannot occur together.

(b)

Compute the value of P (A | B) as follows:

`P(A|B)=(P(A\cap B))/(P(B))=(0)/(0.40)=0`

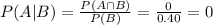
Thus, the value of P (A | B) is 0.

(c)

No, P (A | B) is not equal to the P (A).

(d)

As mentioned in part (a), mutually exclusive events are those events which cannot occur together.

That is,
`P(A\cap B)=0`.

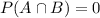Events A and B are independent if the chance of their concurrent happening is equivalent to the multiplication of their distinct probabilities.

That is,
`P(A\cap B)=P(A)* P(B)`.

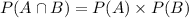The concepts of mutually exclusive events and independent events are not the same.

(e)

As the it is provided that A and B are mutually exclusive events, we know that
`P(A\cap B)=0`.

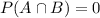Now compute the value of
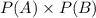`P(A)* P(B)` as follows:

`P(A)* P(B)=0.30* 0.40=0.12\\eq 0`

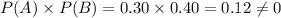
Thus, the events A and B are not independent.

Thus, if two events are mutually exclusive events they cannot be independent.