Answer:
The probability that an individual has this disease given that the test indicates its presence is 0.1
Explanation:
Let A be the event which indicates Having disease
Let B be the event in which test indicates that disease presence
Now we are given that 10% of the individuals in this age group suffer from this form of arthritis
So, P(A)=0.1
We are also given that the proposed test was given to individuals with confirmed arthritics disease, and a correct test result was obtained in 85% of the cases.
P(B|A)=0.85
Now we are given that. When the test was administered to individuals of the same age group who were known to be free of the disease, 4% were reported to have the disease
So,P(B|A')=0.04
We are supposed to find the probability that an individual has this disease given that the test indicates its presence i.e. P(A|B)
So we will use Bayes theorem
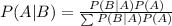
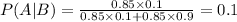
Hence the probability that an individual has this disease given that the test indicates its presence is 0.1