Question

In an accelerated failure test, components are operated under extreme conditions so that a substantial number will fail in a rather short time. In such a test involving two types of microchips, 620 chips manufactured by an existing process were tested, and 125 of them failed. Then, 820 chips manufactured by a new process were tested, and 130 of them failed. Find a 90% confidence interval for the difference between the proportions of failures for chips manufactured by the two processes. (Round the final answers to four decimal places.) The 90% confidence interval is ( . , ).

Answer 1

The 90% confidence interval is
`0.0097 <  p_1 -p_2 < 0.0773`

Explanation:

From the question we are told that

The first sample size is
`n_1 =  620`

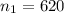
The number of chips that failed is k = 125

The second sample size is
`n_2  =  820`

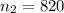
The number of chips that fail is
`u  = 130`

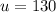
Generally the confidence level is 90% , hence the level of significance is

`\alpha =  (100 - 90)\%`

=>
`\alpha = 0.10`

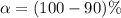
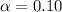
Generally from the normal distribution table the critical value of
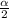`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  1.645`

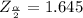
Generally the first sample proportion is

`\r p _1 =  (125)/(620)`

=>
`\r p _1 = 0.202`

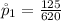
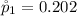
Generally the second sample proportion is

`\r p _1 =  (130)/(820)`

=>
`\r p _1 = 0.1585`

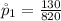
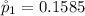
Generally the standard error is mathematically represented as

`SE =  \sqrt{(\r p_1 (1 - \r  p_1))/(n_1) +(\r p_2 (1 - \r  p_2))/(n_2)  }`

=>
`SE =  \sqrt{(0.202(1 - 0.202))/(620) +(0.1585 (1 - 0.1585))/(820)  }`

=>
`SE = 0.0206`

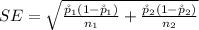
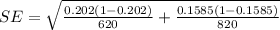
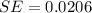
Generally the margin of error is mathematically represented as

`E = Z_{(\alpha )/(2) } * SE`

=>
`E = 1.645 * 0.0206`

=>
`E =0.0338`

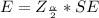
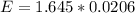
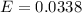
Generally 95% confidence interval is mathematically represented as

`(\r p_1 -\r p_2) -E <  p_1 - p_2 <  (\r p_1 -\r p_2) +E`

=>
`(0.202 -0.1585) -0.0338 <  p_1 - p_2 < (0.202 -0.1585) +0.0338`

=>
`0.0097 <  p_1 - p_2 < 0.0773`