Complete Question
Answer:
a
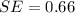
b

Explanation:
From the question we are told that
The sample size is n = 60
The first sample mean is
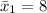
The second sample mean is
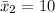
The first variance is
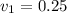
The first variance is
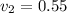
Given that the confidence level is 95% then the level of significance is 5% = 0.05
Generally from the normal distribution table the critical value of
 is
is
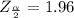
Generally the first standard deviation is
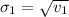
=>
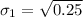
=>

Generally the second standard deviation is
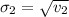
=>
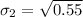
=>
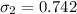
Generally the first standard error is
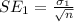
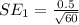
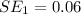
Generally the second standard error is
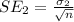
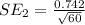
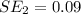
Generally the standard error of the difference between their mean scores is mathematically represented as
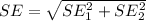
=>
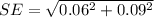
=>
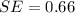
Generally 95% confidence interval is mathematically represented as

=>

=>
