Question

A tennis ball has a diameter of 2.7 inches. The tennis coach wants to fill her storage shed with tennis balls. If the storage shed is 14 feet wide, 15 feet long, and 10 feet high, how many tennis balls will she need to fill up the shed? (Vsphere=43πr3)

Answer 1

Given that,

The diameter of a tennis ball, d = 2.7 inches

Radius, r = 1.35 inches

The dimensions of the storage shed is 14 feet wide, 15 feet long, and 10 feet high.

Volume of the shed is, V = lbh

`V=14* 15* 10\\\\V=2100\ \text{feet}^3`

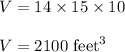
We can convert radius from inches to feet :

1 foot = 12 inches

Radius, r = 0.1125 feet

Let there are x number of tennis balls that can fit in the shed. So,

`x* V_b=V_s\\\\\text{Where}\ V_b\ \text{and}\ V_s\ \text{volume of ball and shed}\\\\x=(V_s)/((4)/(3)\pi r^3)\\\\x=(2100)/((4)/(3)\pi * (0.1125)^3)`

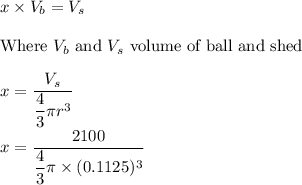
x = 352105.75 balls

or

x = 352106 balls

Hence, 352106 balls can fit in the storage shed.