Question

On the ceiling of a cavern, a stalactite grows downward 0.01 inches per year. Ten feet directly below on the cavern's floor, a stalagmite grows upward 0.005 inches per year. How many years will it take them to meet? Express your answer to the nearest hundredth. Your answer

Answer 1

666.66 years

Explanation:

In this scenario, we need to find at what year both of the stalagmite crystals are at the exact elevation in the cave. So we need an algebraic formula to calculate this. Since the crystal in the ceiling is at a height of 10 feet (height of the cave) and is growing down we need to subtract its growth from its starting position of 10ft. The second crystal is starting at an elevation of 0 and growing upward so we simply need to chart its growth and equal both equations together to find its meet-up point. In this algebraic equation, x will equal the number of years that we need to find.

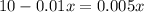`10 - 0.01x = 0.005x` ... add 0.01x to both sides.

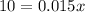`10 = 0.015x` ... divide both sides by 0.015

`666.66 = x`

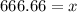
Finally, we can see that both crystals will meet-up after 666.66 years. If we plug this value into the equation we see that the crystals will meet-up at a point 3.33 ft above the cave floor.