Question

A statistician believes that the percent population growth rate of major cities has decreased compared to the last decade. To test his claim, he randomly selects major cities and compares the percent population growth between the years 2007 and 2017 to the percent population growth between the years 1997 and 2007. Suppose that data were collected for a random sample of 17 cities, where each difference is calculated by subtracting the percent growth rate from 1997 to 2007 from the percent growth rate from 2007 to 2017. Assume that the percentages are normally distributed. The statistician uses the alternative hypothesis Ha:μd<0. Using a test statistic of t≈−5.053, which has 16 degrees of freedom, determine the range that contains the p-value.

Answer 1

The range consisting of the p-value is, 0.000001 < p-value < 0.00001.

Explanation:

The dependent t-test (also known as the paired t-test or paired samples t-test) compares the two means associated groups to conclude if there is a statistically significant difference amid these two means.

In this case a paired t-test is used to determine whether the percent population growth rate of major cities has decreased compared to the last decade.

The alternative hypothesis is Hₐ:
`\mu_(d)<0`.

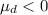The test statistic value is, t = -5.053.

The degrees of freedom is, 16.

Compute the p-value as follows:

`p-value=P(t_(16)<-5.053)=0.000059`

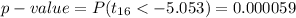
Thus, the range consisting of the p-value is, 0.000001 < p-value < 0.00001.