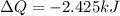Question

5.16 An insulated container, filled with 10 kg of liquid water at 20 C, is fitted with a stirrer. The stirrer is made to turn by lowering a 25-kg object outside the container a distance of 10 m using a frictionless pulley system. The local acceleration of gravity is 9.7 m/s2. Assume that all work done by the object is transferred to the water and that the water is incompressible. A. Determine the work transfer (kJ) to the water. B. Determine the increase in internal energy (kJ) of the water. C. Determine the final temperature ( C) of the water. HINT: Assume that the temperature change is small enough that a constant value of the specific heat is a good approximation. D. Determine the heat transfer (kJ) from the water required to return the water to its initial temperature. Turns, Stephen R.. Thermodynamics (p. 294). Cambridge University Press. Kindle Edition.

Answer 1

a) W=2.425kJ

b)
`\Delta E=2.425kJ`

c)
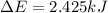
`T_f=20.06^(o)C`

d) Q=-2.425kJ

Step-by-step explanation:

a)

First of all, we need to do a drawing of what the system looks like, this will help us visualize the problem better and take the best possible approach. (see attached picture)

The problem states that this will be an ideal system. This is, there will be no friction loss and all the work done by the object is transferred to the water. Therefore, we need to calculate the work done by the object when falling those 10m. Work done is calculated by using the following formula:

`W=Fd`

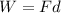
Where:

W=work done [J]

F= force applied [N]

d= distance [m]

In this case since it will be a vertical movement, the force is calculated like this:

F=mg

and the distance will be the height

d=h

so the formula gets the following shape:

`W=mgh`

so now e can substitute:

`W=(25kg)(9.7 m/s^(2))(10m)`

which yields:

W=2.425kJ

b) Since all the work is tansferred to the water, then the increase in internal energy will be the same as the work done by the object, so:

`\Delta E=2.425kJ`

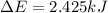
c) In order to find the final temperature of the water after all the energy has been transferred we can make use of the following formula:

`\Delta Q=mC_(p)(T_(f)-T_(0))`

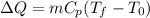
Where:

Q= heat transferred

m=mass

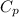`C_(p)`=specific heat

`T_(f)`= Final temperature.

`T_(0)`= initial temperature.

So we can solve the forula for the final temperature so we get:

`T_(f)=(\Delta Q)/(mC_(p))+T_(0)`

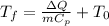
So now we can substitute the data we know:

`T_(f)=(2 425J)/((10000g)(4.1813(J)/(g-C)))+20^(o)C`

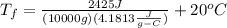
Which yields:

`T_(f)=20.06^(o)C`

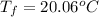
d)

For part d, we know that the amount of heat to be removed for the water to reach its original temperature is the same amount of energy you inputed with the difference that since the energy is being removed this means that it will be negative.

`\Delta Q=-2.425kJ`