Question

Confidence Interval Application Many people feel that the drying of pavement marking paint is much too slow. You spend several days looking for the fastest drying paint you can find; you plan to measure the time (in seconds) for this paint to dry. From information provided by the paint supplier, you believe the time to dry is normally distributed with a standard deviation of 4 seconds. How many paint samples would you need to test to be able to obtain an estimate of paint drying time that is within 1.5 seconds of the actual mean drying time with a probability of 97%

Answer 1

The sample size is
`n =33`

Explanation:

From the question we are told that

The margin of error is E = 1.5 seconds

The standard deviation is s = 4 seconds

Given that the confidence level is 97% then the level of significance is mathematically represented as

`\alpha =( 100 -97)\%`

=>
`\alpha = 0.03`

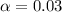
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } =  2.17`

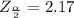
Generally the sample size is mathematically represented as

`n =[ \frac{Z_{(\sigma )/(2 ) } * \sigma }{E} ]^2`

=>
`n =[ (2.17 * 4 )/(1.5) ]^2`

=>
`n =33`