Question

A 50 foot rope weighing a total of 32 lbs extended over a cliff that is 35 feet to the ground. A large 8 pound bucket with 19 gallons of water was tied to the end of the rope at the ground. A group of hikers at the top of the cliff lifted the bucket by pulling up the rope, but when the bucket reached the top, only 12 gallons of water remained (the water spilled out steadily on the way up). If water weighs 8.3 lbs. / gallon. write a function that gives the work required in foot-lbs to lift the bucket up x feet from the ground, and use it to find the work to get the bucket to the top of the cliff.

Answer 1

A function that gives the work required in foot-lbs to lift the bucket up x feet from the ground is
`W=16(50-x)+(19-(x)/(5))(8.3)x` and the work to get the bucket to the top of the cliff is 3726 foot-lbs

Explanation:

Work done to lift the rope by distance x feet:

`W_1=32((50-x)/(2))`

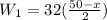
Work done to lift the bucket by distance x feet:

`W_2=(19-(x)/(5))(8.3)x`

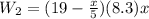
On reaching top 7 gallons of water spilled out so , on going up by x feet
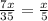`(7x)/(35)=(x)/(5)` gallons of water spilled out.

a function that gives the work required in foot-lbs to lift the bucket up x feet from the ground:

`W=16(50-x)+(19-(x)/(5))(8.3)x`

Now the work to get the bucket to the top of the cliff i.e. x =35

`W=16(50-35)+(19-(35)/(5))(8.3)(35)`

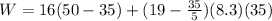
W=3726

Hence, a function that gives the work required in foot-lbs to lift the bucket up x feet from the ground is
`W=16(50-x)+(19-(x)/(5))(8.3)x` and the work to get the bucket to the top of the cliff is 3726 foot-lbs