Question

The titanium shell of an SR-71 airplane would expand when flying at a speed exceeding 3 times the speed of sound. If the skin of the plane is 400 degrees C and the linear coefficient of expansion for titanium is 5x10 -6 /C when flying at 3 times the speed of sound, how much would a 10-meter long (originally at 0C) rod portion (1-dimension) of the airplane expand?

Answer 1

The 10-meter long rod of an SR-71 airplane expands 0.02 meters (2 centimeters) when plane flies at 3 times the speed of sound.

Step-by-step explanation:

From Physics we get that expansion of the rod portion is found by this formula:

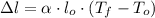`\Delta l = \alpha\cdot l_(o)\cdot (T_(f)-T_(o))` (Eq. 1)

Where:

`\Delta l` - Expansion of the rod portion, measured in meters.

`\alpha` - Linear coefficient of expansion for titanium, measured in
`(1)/(^(\circ)C)`.

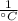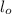`l_(o)` - Initial length of the rod portion, measured in meters.

`T_(o)` - Initial temperature of the rod portion, measured in Celsius.

`T_(f)` - Final temperature of the rod portion, measured in Celsius.

If we know that
`\alpha = 5* 10^(-6)\,(1)/(^(\circ)C)`,
`l_(o) = 10\,m`,
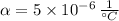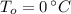`T_(o) = 0\,^(\circ)C` and
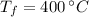`T_(f) = 400\,^(\circ)C`, the expansion experimented by the rod portion is:

`\Delta l = \left(5* 10^(-6)\,(1)/(^(\circ)C) \right)\cdot (10\,m)\cdot (400\,^(\circ)C-0\,^(\circ)C)`

`\Delta l = 0.02\,m`

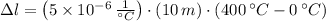
The 10-meter long rod of an SR-71 airplane expands 0.02 meters (2 centimeters) when plane flies at 3 times the speed of sound.