Question

EJERCICIOS: Resuelvan los problemas aplicando regla de tres en conversion de metros a varas A) Una mesa cuadrada mide 1.85 M de lado ¿ cuantas varas debe tener cada tabla de largo para fabricarla? B) Jose tiene un lote de 25 M de largo y 15 M de ancho ¿cuantas varas cuadradas tiene el terreno? Por favor ayuda es para ahorita si mo saben no contesten ok por favor gracias

Answer 1

A) Se requiere una tabla con una longitud de 2.213 varas para fabricar la mesa.

B) El lote de José tiene una extensión de 536.481 varas cuadradas.

Explanation:

A) La vara es una unidad de longitud equivalente a 0.836 metros. También sabemos que un cuadrado es una figura geométrica con cuatro lados de igual longitud y cuatro ángulos rectos, de modo que la longitud y ancho de la mesa es igual. Entonces, el largo de la tabla, esto es, la superficie superior de la mesa, tiene una medida de 1.85 metros.

A continuación, realizamos la regla de tres para determinar su equivalente en varas:

`x = 1.85\,m*(1\,vara)/(0.836\,m)`

`x = 2.213\,varas`

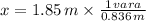
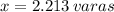
Se requiere una tabla con una longitud de 2.213 varas para fabricar la mesa.

B) La vara es una unidad de longitud equivalente a 0.836 metros. Una vara cuadrada es una unidad de área y es igual a:

`r = (0.836\,m)\cdot (0.836\,m)`

`r = 0.699\,m^(2)`

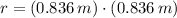
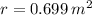
De manera semejante, tenemos que el área del lote de Jose es un rectángulo y que se calcula como sigue en metros cuadrados:

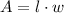`A = l\cdot w` (Eq. 1)

Donde:

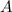`A` - Área del lote de José, medido en metros cuadrados.

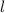`l` - Largo del lote de José, medido en metros cuadrados.

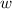`w` - Ancho del lote de José, medido en metros cuadrados.

Si
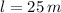`l = 25\,m` y
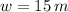`w = 15\,m`, entonces el área del lote es:

`A = (25\,m)\cdot (15\,m)`

`A = 375\,m^(2)`

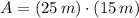
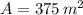
Por último, hallamos el área en varas cuadradas mediante la siguiente regla de tres:

`x = 375\,m^(2)* (1\,vara)/(0.699\,m^(2))`

`x = 536.481\,varas^(2)`

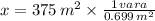
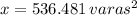
El lote de José tiene una extensión de 536.481 varas cuadradas.