Question

Sarah throws a ball directly upward at the edge of a cliff with a starting velocity of 3.0 \, \dfrac{\text m}{\text s}3.0 s m ​ 3, point, 0, start fraction, start text, m, end text, divided by, start text, s, end text, end fraction. It lands on the ground with a final speed of 6.0 \, \dfrac{\text m}{\text s}6.0 s m ​ 6, point, 0, start fraction, start text, m, end text, divided by, start text, s, end text, end fraction. How long is the ball in the air?

Answer 1

Answer: t= 0.92 s

Explanation: the formula you use it’s v=vinitial + at and you rearrange it to make (t= vfinal - vinitial /a) using this you get 0.92s

Answer 2

t = 0.3 seconds

Step-by-step explanation:

Given that,

Initial velocity of a ball, u = 3 m/s

Final velocity of the ball, v = 6 m/s

We need to find the time for which the ball is in the air. As the ball was directed upwards, it would mean that the acceleration of the ball is -g or -9.8 m/s².

Using the first equation of motion to find the time. So,

v=u+at

or

v=u-gt

`t=(v-u)/(-g)\\\\t=(6-3)/(-9.8)\\\\t=-0.3\ s`

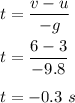
or

t = 0.3 seconds

So, the ball is in the air for 0.3 seconds.