Question

Los siguientes problemas se encuentran en lenguaje común, traduzcan cada uno de ellos a lenguaje algebraico solamente. AEel cuadrado de un número menos cinco es igual a doscientos veinte B) Alejandra pensó un número, lo elevó al cuadrado, multiplicó el resultado por cuatro y obtuvo cien C)Si una pista de baile tiene un área de 5625m² y se sabe que su largo mide lo mismo que su ancho, cuanto medirán las dimensiones de la pista de baile

Answer 1

A) La traducción algebraica de la oración es
`x^(2)-5=220`.

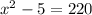B) La traducción algebraica de la oración es
`4\cdot x^(2) = 100`.

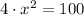C) Ese problema se traduce bajo esta forma lógica como
`w\cdot l = 5625\,m^(2)`
`\land`
`w = l`
`\implies`
`w = 75\,m`
`\land`
`l = 75\,m`.

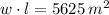
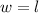
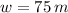
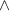
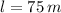Explanation:

Debemos proceder en este ejercicio como sigue:

1) Leer cuidadosamente la frase.

2) Escribir su equivalente matemático a medida que se lee y hasta culminarlo.

A continuación, presentamos el desarrollo y la conclusión de cada ejercicio:

A) Interpretamos la oración paso a paso conforme al lenguaje matemático conocido:

(i) El cuadrado de un número:

`x^(2)`

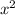
(ii) El cuadrado de un número menos cinco:

`x^(2)-5`

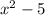
(iii) El cuadrado de un número menos cinco es igual a:

`x^(2)-5=`

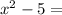
(iv) El cuadrado de un número menos cinco es igual a doscientos veinte:

`x^(2)-5=220`

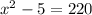
La traducción algebraica de la oración es
`x^(2)-5=220`.

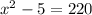B) Interpretamos la oración paso a paso conforme al lenguaje matemático conocido:

(i) Alejandra pensó un número:

`x`

(ii) Alejandra pensó un número, lo elevó al cuadrado,:

`x^(2)`

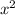
(iii) Alejandra pensó un número, lo elevó al cuadrado, multiplicó el resultado por cuatro:

`4\cdot x^(2)`

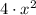
(iv) Alejandra pensó un número, lo elevó al cuadrado, multiplicó el resultado por cuatro y obtuvo cien:

`4\cdot x^(2) = 100`

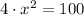
La traducción algebraica de la oración es
`4\cdot x^(2) = 100`.

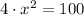C) Interpretamos la oración paso a paso conforme al lenguaje matemático conocido:

(i) Si una pista de baile tiene un área de 5625 m²:

`A = 5625\,m^(2)`

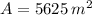
(ii) Si una pista de baile tiene un área de 5625 m² y se sabe que su ancho mide lo mismo que su ancho:

Lo que se infiere de la afirmación es que la pista de baile sería un cuadrilátero y más precisamente, un cuadrado:

`A = 5625\,m^(2)`

`A = w\cdot l` (
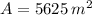
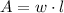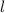`l` - Largo,
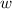`w` - Ancho)

`w = l`

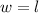
Entonces la ecuación algebraica sería:

`l^(2) = 5625\,m^(2)`

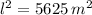
(iii) Si una pista de baile tiene un área de 5625 m² y se sabe que su ancho mide lo mismo que su ancho, cuanto medirán las dimensiones de la pista de baile:

Lo que se infiere de la afirmación es que la pista de baile sería un cuadrilátero y más precisamente, un cuadrado:

`A = 5625\,m^(2)`

`A = w\cdot l` (
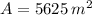
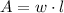`l` - Largo,
`w` - Ancho)

`w = l`

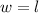
Entonces la ecuación algebraica sería:

`l^(2) = 5625\,m^(2)`

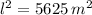
Y obtenemos la longitud por despeje:

`l = \sqrt{5625\,m^(2)}`

`l = 75\,m`

`w = 75\,m`

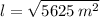
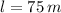
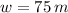
Ese problema se traduce bajo esta forma lógica como
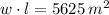
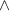
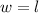
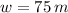
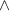
`w\cdot l = 5625\,m^(2)`
`\land`
`w = l`
`\implies`
`w = 75\,m`
`\land`
`l = 75\,m`.