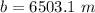Answer:
a
The hiker (you ) is 200 m below his/her(your) starting point
b
The resultant displacement in the north east direction is
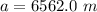
The resultant displacement in vertical direction (i.e the altitude change )
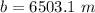
Step-by-step explanation:
From the question we are told that
The displacement in the morning is
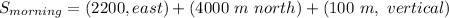
The displacement in the afternoon is
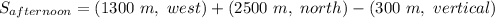
Generally the direction west is negative , the direction east is positive
the direction south is negative , the direction north is positive
resultant displacement is mathematically evaluated as
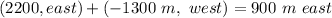
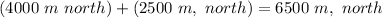

From the above calculation we see that at the end of the hiking the hiker (you) is 200 m below his/her(your) initial position
Generally from Pythagoras theorem , the resultant displacement in the north east direction is
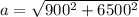
=>
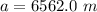
Generally from Pythagoras theorem , the resultant displacement in vertical direction (i.e the altitude change )
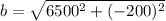
=>