Question

A clothing store owner decided to track customers' reasons for returning items. She found that 9% of customers do not provide a reason, 29% say the item did not fit, 13% find a flaw with the item and 4% changed their mind about the purchase. The remaining customers returns gifts purchased for them. What is the probability that out of 40 returns on a given day, 20 are gifts that are being returned?

Answer 1

0.102542

Explanation:

Given that 9% of customers do not provide a reason, 29% say the item did not fit, 13% find a flaw with the item, and 4% changed their mind about the purchase.

So, the total percentage of items returned due to no reason, unfit, flaw, and due to changing mind

=9%+29%+13%+4%=55%

As the remaining customers returned gifts purchased for them, so, the percentage of customers who returned gifts =100-55=45%.

So, the fraction of customers who returned gifts=45/100=0.45.

Now, observe that if 1 item returned, there is a chance of 0.45 that the item is a gift.

Moreover, there are only two possibilities for any idem, i.e the idem was a gift or not a gift, so the number of total returned items can be considered a Bernoulli's population.

Let p be the probability of a returned item which is the same for all the returned items,

p=0.45

So, according to Bernoulli's theorem, the probability that out of n=40 returns on a given day, r=20 are gifts is

`\binom{n}{r}p^r(1-p)^(n-r)=\binom{40}{20}(0.45)^(20)(1-0.45)^(40-20)`

`=0.102542`

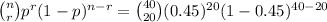
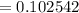
Hence, the probability that 20 returned items are gifts among the total 40 returned items is 0.102542.