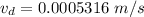Complete Question
A number 14 copper wire has a diameter of 1.628 mm. Calculate the resistance of a 37.0 m long piece of such wire.
(Use 1.72×10-8 ?m for the resistivity of copper.)
For safety, the National Electrical Code limits the allowable amount of current which such a wire may carry. When used in indoor wiring, the limit is 15.0 A for rubber insulated wire of that size. How much power would be dissipated in the wire of the above problem when carrying the maximum allowable current?
What would be the voltage between the ends of the wire in the above problem?
What is the current density in the wire when it is carrying the maximum allowable current? (Current density is the current in the wire divided by the cross sectional area of the wire.)
What is the drift velocity of the electrons when the wire is carrying the maximum allowable current?
(The density of electrons in copper is 8.47×1028 m-3.)
Answer:
a
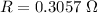
b
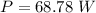
c
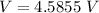
d
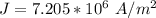
e
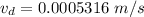
Step-by-step explanation:
From the question we are told that
The resistivity of copper is
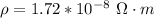
The current limit is
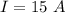
The diameter is

The length of the wire is
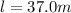
The density of electron is

Generally the radius is mathematically represented as
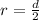
=>
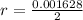
=>
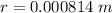
Generally the resistance is mathematically represented as
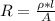
Here A is the area which is mathematically represented as
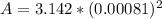
=>
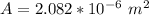
=>
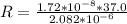
=>
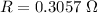
Generally the power dissipated is mathematically represented as
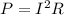
=>
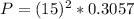
=>
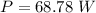
Generally the voltage is mathematically represented as

=>

=>
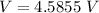
Generally the charge density is mathematically represented as

=>
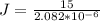
=>
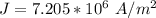
Generally the drift velocity is mathematically represented as
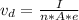
Here e is the charge on an electron with value

So

=>

=>