Question

A culture of bacteria has an initial population of 12000 bacteria and doubles every 6 hours. Using the formula P_t = P_0\cdot 2^{\frac{t}{d}}P t ​ =P 0 ​ ⋅2 d t ​ , where P_tP t ​ is the population after t hours, P_0P 0 ​ is the initial population, t is the time in hours and d is the doubling time, what is the population of bacteria in the culture after 17 hours, to the nearest whole number?

Answer 1

Answer:Pt 85526.2769 = 85526

Explanation:

Answer 2

85,524 bacteria

Explanation:

Given the population of bacteria modelled by the equation where;

`P_t = P_0\cdot 2^{(t)/(d)`

P0 is the initial population

t is the time in hours

d is the doubling time

If the culture of bacteria has an initial population of 12000 bacteria, this means that;

at t = 0, P0 = 12000

substitute into the modelled function

`P_t = P_0\cdot 2^{(t)/(d)\\\\P_t = 12000\cdot 2^{(0)/(d)\\\\\\P_t =12000\cdot 2^(0)\\\\P_t = 12000`

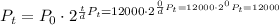
If the population doubles every 6 hours

at t = 6, Pt = 24000

`P_t = P_0\cdot 2^{(t)/(d)\\\\\\24000 = 12000\cdot 2^{(6)/(d)\\\\\\\\24000/12000 = 2^{(6)/(d)\\\\\\\\`

`2 = 2^{(6)/(d) }\\1 = 6/d\\d = 6\\`

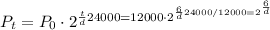
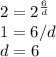
Next is to get the population of bacteria in the culture after 17 hours

at t = 17, Pt = ?

`P_t = P_0\cdot 2^{(t)/(d)\\\\P_t = 12000\cdot 2^{(17)/(6)\\\\\\\\P_t = 12000\cdot 2^( 2.833 )\\P_t = 12000\cdot 2^( 2.833 )\\P_t = 12000 * 7.127\\P_t = 85,524.3`

Hence the population of bacteria in the culture after 17 hours, to the nearest whole number is 85,524 bacteria