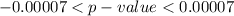Question

A real estate agent believes that the value of houses in the neighborhood she works in has increased from last year. To test this claim, she selects random houses in this neighborhood and compares their estimated market value in the current year to their estimated market value in the previous year. Suppose that data were collected for a random sample of 8 houses, where each difference is calculated by subtracting the market value of the previous year from the market value of the current year. Assume that the values are normally distributed. The agent uses the alternative hypothesis Ha:μd>0. Using a test statistic of t≈7.496, which has 7 degrees of freedom, determine the range that contains the p-value.

Answer 1

The range is
`-0.00007 < p-value < 0.00007`

Explanation:

From the question we are told that

The sample size is n = 8

The null hypothesis is
`H_o : \mu_d = 0`

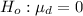
The alternative hypothesis is
`H_a : \mu_d > 0`

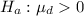
The test statistics is
`z \approx 7.496`

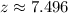
The degree of freedom is
`df = 7`

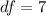
Generally the p-value is mathematically represented as

`p-value = P(Z > 7.496 )`

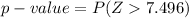
Generally from the t distribution table

(Reference -

danielsoper(dot)com(slash)statcalc(slash)calculator)

the value of
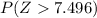`P(Z > 7.496 )` at a degree of freedom 7 is

`P(Z > 7.496 ) = t_(7.496 , 7 ) =0.00007`

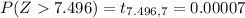
So the range that contains the p -value is

`-0.00007 < p-value < 0.00007`