Question

Enter the first 4 terms of the sequence defined by the given rule. Assume that the domain of each function is the set of whole numbers greater than 0.


`f(n) =3 {n}^(2) + 1`
​

Answer 1

Given:

The rule for the sequence is

`f(n)=3n^2+1`

Domain of the function is the set of whole numbers greater than 0.

To find:

The first 4 terms of the sequence defined by the given rule.

Solution:

We have,

`f(n)=3n^2+1`

Domain of the function is the set of whole numbers greater than 0. So, domain for first four terms are 1, 2, 3 and 4 respectively.

For n=1,

`f(1)=3(1)^2+1`

`f(1)=3(1)+1`

`f(1)=3+1`

`f(1)=4`

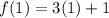
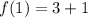
For n=2,

`f(2)=3(2)^2+1`

`f(2)=3(4)+1`

`f(2)=12+1`

`f(2)=13`

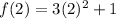
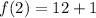
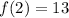
For n=3,

`f(3)=3(3)^2+1`

`f(3)=3(9)+1`

`f(3)=27+1`

`f(3)=28`

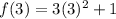
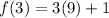
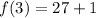
For n=4,

`f(4)=3(4)^2+1`

`f(4)=3(16)+1`

`f(4)=48+1`

`f(4)=49`

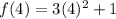
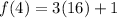
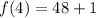
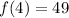
Therefore, the first 4 terms of the sequence defined by the given rule are 4, 13, 28 and 49 respectively.