Question

Line M passes through points (2,-5) and (4, -3). Line N passes through points (-4, -8) and (-6,-6). Are lines M and N perpendicular? Explain.

A. No, the lines are not perpendicular because the product of their slopes equals -1.

B. Yes, the lines are perpendicular because the product of their slopes equals-1.

C. No, their lines are not perpendicular because the product of their slopes does not equal-1.

D. Yes, the lines are perpendicular because the product of their slopes does not equal -1.

Answer 1

Yes, the lines are perpendicular because the product of their slopes equals -1 ⇒ B

Explanation:

The product of the slopes of the perpendicular lines is -1

So to prove that the lines are perpendicular let us find their slopes

The rule of the slope is:

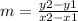`m=(y2-y1)/(x2-x1)` , where (x1, y1) and (x2, y2) are two points on the line

∵ Line M passes through points (2, -5) and (4, -3)

∴ x1 = 2 and x2 = 4

∴ y1 = -5 and y2 = -3

→ By using the rule of the slope above

∴
`m=(-3-(-5))/(4-2)=(-3+5)/(2)=(2)/(2)`

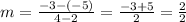
∴ The slope of line M is 1

∵ Line N passes through points (-4, -8) and (-6, -6)

∴ x1 = -4 and x2 = -6

∴ y1 = -8 and y2 = -6

→ By using the rule of the slope above

∴
`m=(-6-(-8))/(-6-(-4))=(-6+8)/(-6+4)=(2)/(-2)`

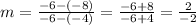
∴ The slope of line N is -1

∵ 1 × -1 = -1

∴ The product of the slopes of lines M and N is -1

∴ Lines M and N are perpendicular

∴ Yes, the lines are perpendicular because the product of their

slopes equals -1.