1 Answer

Rafael Medeiros · Answer 1 · 2021-03-30T09:58:09+0000

Given:

The measure of the first angle is 40° less than the measure of the second.

To find:

The measures of the complementary angles that satisfy the given condition.

Solution:

Let the measure of first angle be x°.

According to the given condition,

First angle = Second angle - 40°

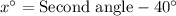
$x^\circ =\text{Second angle}-40^\circ$

Add 40° on both sides.

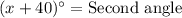
$(x+40)^\circ =\text{Second angle}$

We know that, sum of complementary angles is 90°. So,

First angle + Second angle = 90°

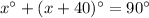
$x^\circ +(x+40)^\circ =90^\circ$

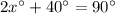
$2x^\circ +40^\circ =90^\circ$

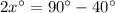
$2x^\circ =90^\circ -40^\circ$

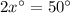
$2x^\circ =50^\circ$

Divide both sides by 2.

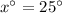
$x^\circ =25^\circ$

So, the measure of first angle is 25°.

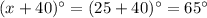
$(x+40)^\circ =(25+40)^\circ =65^\circ$

So, the measure of second angle is 65°.

Please log in or register to add a comment.