Question

What is an equation of the line that passes through the points (0, 3) and (5,-3)?

Put your answer in fully reduced form.

Answer 1

The equation of the line that passes through the points (0, 3) and (5, -3) is
`y = -(6)/(5)\cdot x +3`.

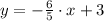Explanation:

From Analytical Geometry we must remember that a line can be formed after knowing two distinct points on Cartesian plane. The equation of the line is described below:

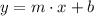`y = m\cdot x + b` (Eq. 1)

Where:

`x` - Independent variable, dimensionless.

`y` - Dependent variable, dimensionless.

`m` - Slope, dimensionless.

`b` - y-Intercept, dimensionless.

If we know that
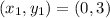`(x_(1),y_(1)) = (0,3)` and
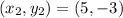`(x_(2),y_(2))=(5,-3)`, the following system of linear equations is constructed:

`b = 3` (Eq. 2)

`5\cdot m + b = -3` (Eq. 3)

The solution of the system is:
`b = 3`,
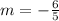`m = -(6)/(5)`. Hence, we get that equation of the line that passes through the points (0, 3) and (5, -3) is
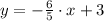`y = -(6)/(5)\cdot x +3`.