Question

Find the distance between Line c and Point A. Round to
the nearest tenth.

Answer 1

The distance is approximately 3.6

Explanation:

The distance from a point (xo, yo) to a line ax+by+c=0 is the shortest distance from the given point to any point on the line.

It can be calculated with the formula:

`\displaystyle d={\frac {\mid ax_(0)+by_(0)+c\mid}{\sqrt {a^(2)+b^(2)}}}`

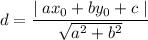
The coordinates of point A are (1,-2). The equation of the line must be found by knowing two clear points it passes through.

These points are (0,3) and (6,-1). First, we calculate the slope:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

`\displaystyle m=(-1-3)/(6-0)=(-4)/(6)=-(2)/(3)`

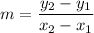
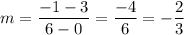
The equation of the line in slope-point form is:

`y=m(x-x_o)+y_o`

Taking the point (0,3) and the slope above:

`\displaystyle y=-(2)/(3)(x-0)+3`

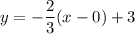
Multiply by 3:

`3y=-2x+9`

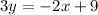
Moving all terms to the left side:

`2x+3y-9=0`

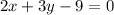
We now have all the required values to calculate the distance:

a=2, b=3, c=-9, xo=1, yo=-2

`\displaystyle d={\frac {\mid 2\cdot 1+3\cdot (-2)+(-9)\mid}{\sqrt {2^(2)+3^(2)}}}`

`\displaystyle d={\frac {\mid 2-6-9\mid}{\sqrt {13}}}\approx 3.61`

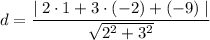
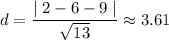
The distance is approximately 3.6