Answer:

Explanation:
We need to find the equation of the line perpendicular to the line 3x+2y=8 and passes through (-5,2).
The given line can be expressed as:
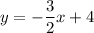
We can see the slope of this line is m1=-3/2.
The slopes of two perpendicular lines, say m1 and m2, meet the condition:
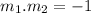
Solving for m2:
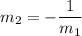
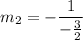
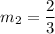
Now we know the slope of the new line, we use the slope-point form of the line:
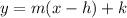
Where m is the slope and (h,k) is the point. Using the provided point (-5,2):
