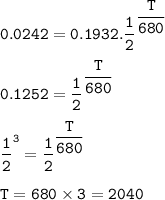Question

A sample contains 2.2 g of the radioisotope niobium-91 and 15.4 g of its daughter isotope, zirconium-91.

If the half-life of niobium-91 is 680 years, how long will it take for the decay described in the previous question?

680 years
1,360 years
✓2,040 years (correct answer)
2,720 years

Answer 1

It’s CCCCCCCCCCCCCCC

Step-by-step explanation:

I just took the instruction and yes its “C.”

Answer 2

Time to decay : 2040 years

Further explanation

The atomic nucleus can experience decay into 2 particles or more due to the instability of its atomic nucleus.

Usually radioactive elements have an unstable atomic nucleus.

The main particles are emitted by radioactive elements ,so that they generally decay, are alpha (α), beta (β) and gamma (γ) particles

General formulas used in decay:

`\tt Nt=No.(1)/(2)^{(T)/(t(1)/(2) )`

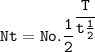
T = duration of decay

t 1/2 = half-life

N₀ = the number of initial radioactive atoms

Nt = the number of radioactive atoms left after decaying during T time

moles zirconium :

`\tt (15.4)/(91)=0.169`

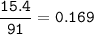
moles niobium :

`\tt (2.2)/(91)=0.0242`

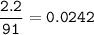
the half-life of niobium-91 is 680 years

Reaction

⁹¹₄₁Nb ⇒⁹¹₄₀Zr + ₁⁰e

Amount of Nb from reaction : 0.169

Amount of initial Nb = 0.0242 + 0.169 = 0.1932

Time to decay (T) :

`\tt 0.0242=0.1932.(1)/(2)^{(T)/(680)}\\\\0.1252=(1)/(2)^{(T)/(680)}\\\\(1)/(2)^(3)=(1)/(2)^{(T)/(680)}\\\\T=680* 3=2040`