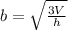Question

Solve the formula V = 1/3b^2 h for b.

Answer 1

`b=\sqrt{(3V)/(h)}`

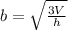
Explanation:

To solve a formula for one of its variables do that

• Underline the variable

• Separate it on one side and the other terms on the other side

• Make its coefficient equals 1

Let us use these steps to solve our question

∵ V =
`(1)/(3)` b²h

→ Underline b

∴ V =
`(1)/(3)` b²h

→ Multiply both sides by 3 to cancel the denominator on the right side

∴ 3V = b²h

→ Divide both sides by h to move it to the other side

∴
`(3V)/(h)=b^(2)`

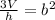
→ To find b take √ for both sides

∴
`\sqrt{(3V)/(h)}=\sqrt{b^(2) }`

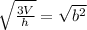
→ The square root will cancel the power 2 of b

∴
`\sqrt{(3V)/(h)}=b`

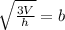
→ Switch the two sides

∴
`b=\sqrt{(3V)/(h)}`