Question

You would like to know whether forwards in a basketball league average the same (or different) numbers of points than the overall league average of 7.5 points. Drawing a random sample of 10 forwards from the league, their averages were: 10, 9, 6, 11, 13, 14, 9, 9, 9, and 10 points. If you were going to compare the obtained average of scoring by the sampled forwards with the population value of 7.5.

Required:
What is the critical t-value for such a test given an alpha level of 0.05?

Answer 1

The critical t-value for such a test given an alpha level of 0.05 is 2.26

Explanation:

Null hypothesis :
`H_0:\mu = 7.5`

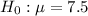
Alternate hypothesis :
`H_a:\mu \\eq 7.5`

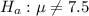
Population mean =
`\mu = 7.5`

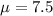
Data : 10, 9, 6, 11, 13, 14, 9, 9, 9, and 10

Mean =
`\bar{x}=\frac{\text{Sum of all observations}}{\text{no. of observations}}`

Mean =
`(10+9+6+11+13+14+9+9+ 9+ 10)/(10)`

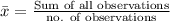
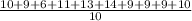
Mean =10

Standard deviation :
`\sqrt{\frac{\sum(x-\bar{x})^2}{n}}`

Standard deviation :
`\sqrt{((10-10)^2+(9-10)^2+(6-10)^2+(11-10)^2+(13-10)^2+(14-10)^2+(9-10)^2+(9-10)^2+(9-10)^2+(10-10)^2)/(10)}`

Standard deviation s :2.144

`t = (x-\mu)/((s)/(√(n)))t = (10-7.5)/((2.144)/(√(10)))t=3.687`

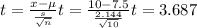
Df = n-1 = 10-1 = 9

T critical =
`t_((df,\alpha))=t_(9,0.05)=2.26`

T calculated > T critical

So, We failed to accept null hypothesis

Hence the critical t-value for such a test given an alpha level of 0.05 is 2.26